Zeilenbild
Gegeben:
- lineare Gleichungen
- Unbekannte in den Gleichungen
- mit
Beispiel: (Lineares Gleichungssystem mit
Matrixform:
- erster Teil =
- zweiter Teil =
- dritter Teil =
Graphische Darstellung:
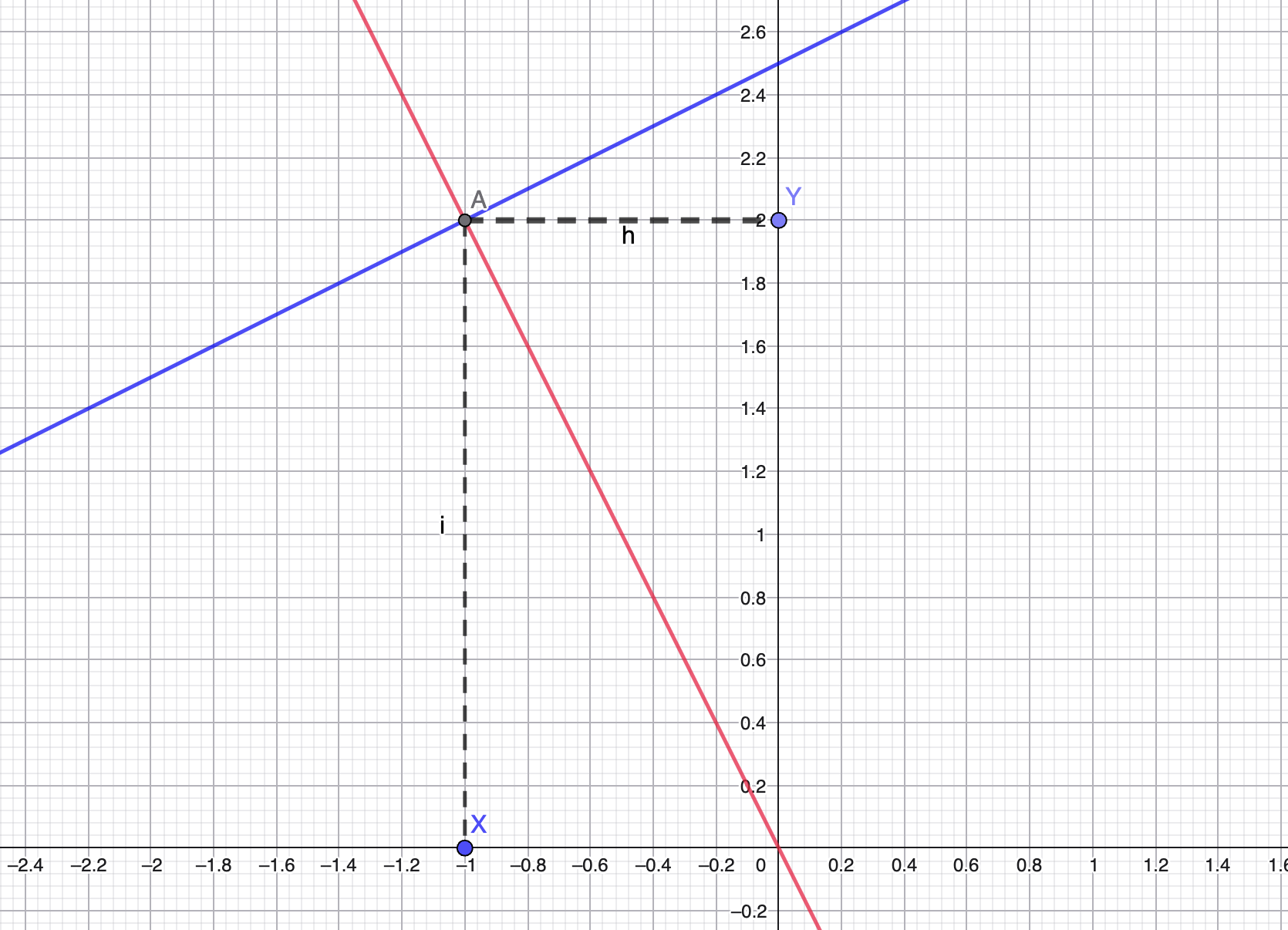
erfüllen beide lineare Gleichungen
Spaltenbild
- Man sucht die richtige Zahlen für und , sodass die die Summe von und die Spalte ergibt
- Gelöst wird das ganze mit und
Linearkombination
Wenn Spalten gegeben sind also so nennen wir diese Verknüpfung
mit Zahlen eine Linearkombination dieser Spalten
Graphische Darstellung
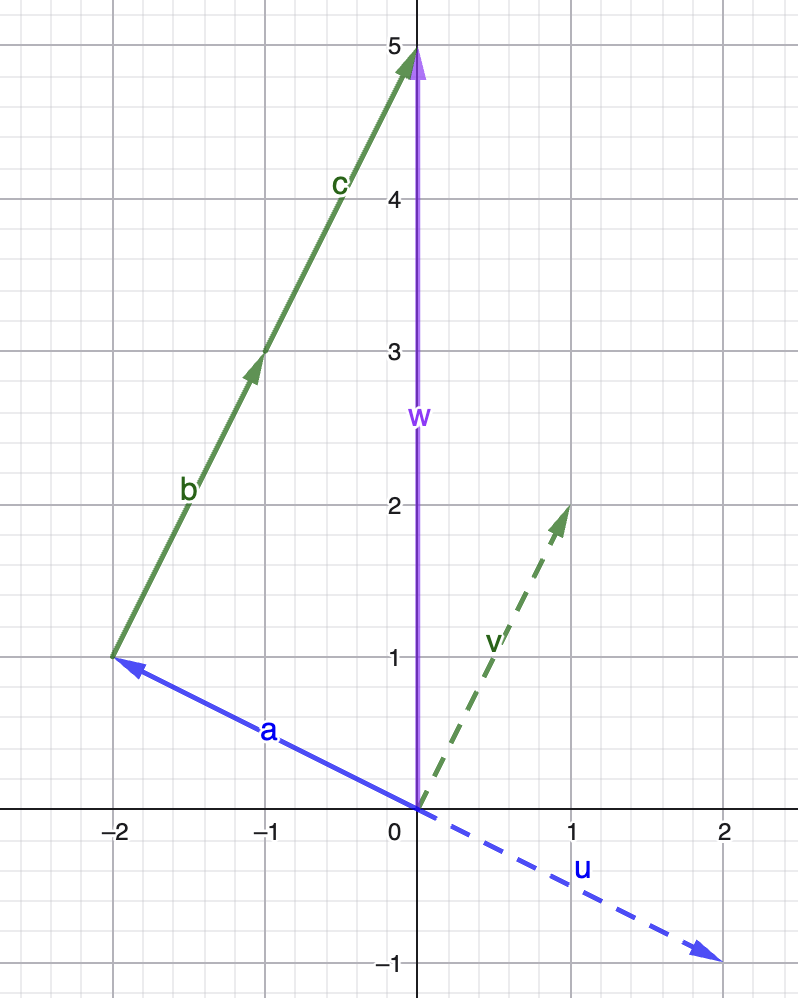 Man sieht, dass wir -1 mal x verwenden (blau) und 2 mal y (grün) und kommen damit auf die Spalte
Man sieht, dass wir -1 mal x verwenden (blau) und 2 mal y (grün) und kommen damit auf die Spalte
Lineare Gleichungssysteme mit
Bsp.:
Matrixform:
Als Zeilenbild
1. Zeile bildet eine Ebene, da man irgendeinen Wert für einsetzen kann 3. Zeile bildet eine Ebene, da man irgendeinen Wert für einsetzen kann
Graphische Darstellung:
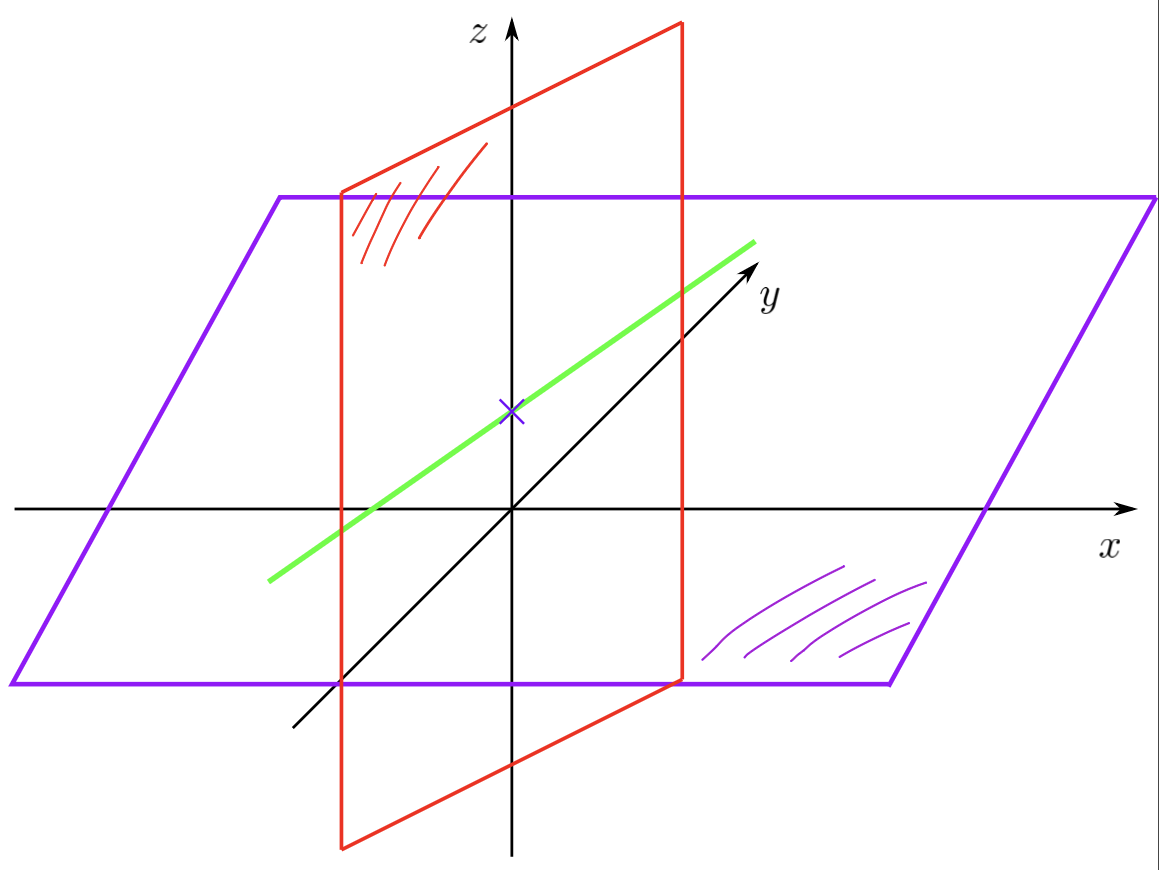 Nun nimmt man die Gerade an der sich die 2 Ebenen schneiden und zeichnet die 2. Ebene ein um den genauen Schnittpunkt zu erkennen
Nun nimmt man die Gerade an der sich die 2 Ebenen schneiden und zeichnet die 2. Ebene ein um den genauen Schnittpunkt zu erkennen
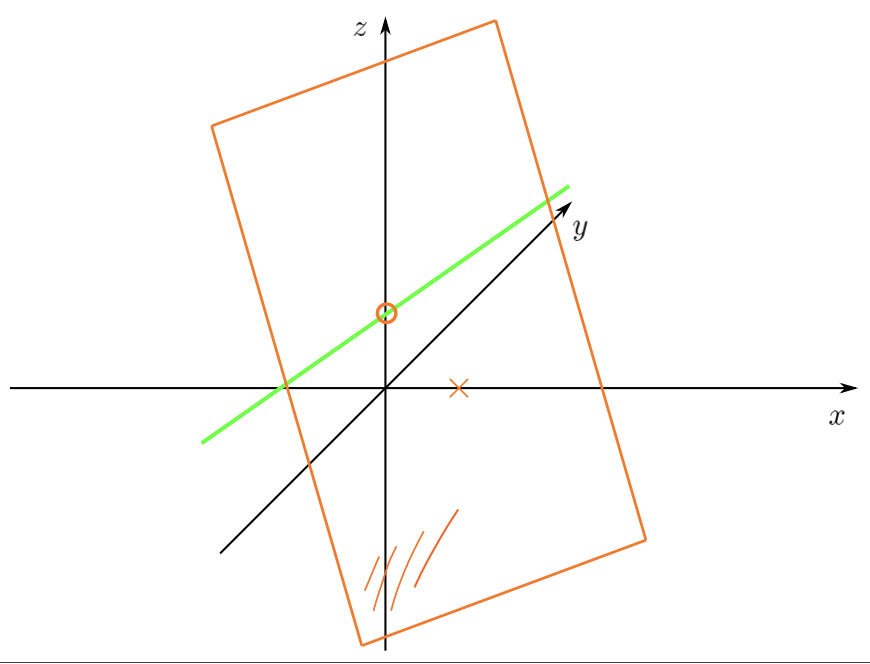 Man sieht, dass sich der Schnittpunkt bei (0, 0, 0) befindet
Auch erkennt man, dass es bei höheren immer unübersichtlicher wird. Ab nicht mehr vorstellbar
Man sieht, dass sich der Schnittpunkt bei (0, 0, 0) befindet
Auch erkennt man, dass es bei höheren immer unübersichtlicher wird. Ab nicht mehr vorstellbar
Als Spaltenbild
Wir müssen nun für , und so die Werte einsetzen, damit die Summe der Spalten die Spalte ergibt Beim genauen hinschauen erkennen wir, dass den selben Wert wie die Spalte besitzt Damit können wir sagen, dass wir für und 0 einsetzen können und für damit das Gleichungssystem gelöst ist
Graphische Darstellung:
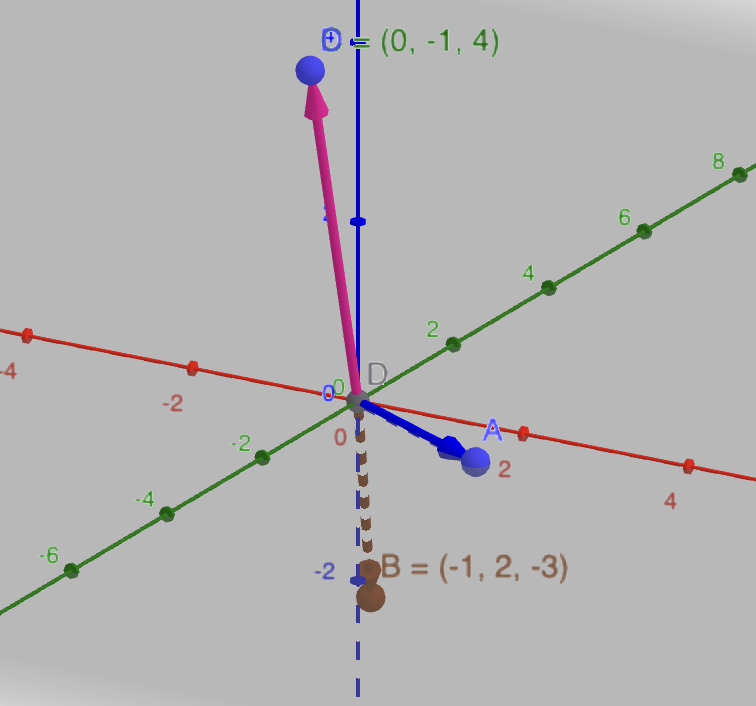 Anmerkung: (Man sieht nicht, da er in ist, Punkt D)
Anmerkung: (Man sieht nicht, da er in ist, Punkt D)
- Wenn wir eine neue Spalte haben, müssen wir die Linearkombination von neu lösen
Bsp.: (mit den alten Spalten)
Beim genauerem hinsehen erkennen wir, dass wir für und einsetzen müssen damit wir auf kommen. Für
 zeigt auf den Punkt D
zeigt auf den Punkt D
Kann man jede neue Spalte berechnen?
Als Spaltenbild
Spaltenbild
ist die Linearkombination der Spalten der Matrix
Mit der Matrix
Bsp.: Neue Spalte berechnen, die sich aus ergibt
Als Zeilenbild
Zeilenbild
zeilenweise Produkt berechnen
mit der Matrix
Bsp.: Neue Spalte berechnen, die sich aus ergibt
Wann ist es nicht möglich auf die Spalte zu kommen?
Bsp.:
Wir sehen, dass die Spalten 1 und 2 bei gleich bzw. Vielfache voneinander sind Alle Spalten sind Linearkombination von
Lineare Abhängigkeit
Wenn mindestens eine Spalte die Linearkombination von einer anderen ist, so ist die Menge der Spalten linear abhängig Ansonsten immer *linear unabhängig
Lösbarkeit von Linearen Gleichungssystem
Die Gleichung kann nur eindeutig auf ein gelöst werden, wenn die Spalten von linear unabhängig ist