Allgemein
Wir können durch benachbarte Einträge Minimierungen durchführen, was zu einer Optimierung des Schaltnetzes führen kann. Dies funktioniert nur wenn sie sich durch einen Wert einzigen unterscheiden
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Benachbarter Eintrag mit nur einer Unterscheidung
Karnaugh-Veitch-Diagramm (KV-Diagramm)
Mit dem KV-Diagramm können wir die Minimierung einfacher gestalten
1. KV-Diagramm aufstellen
Man sollte die Elemente so aufstellen, dass sie ich jeweils gegenseitig nur um 1 Bit unterscheiden.
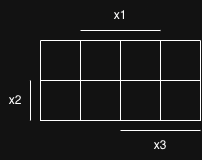
2. Zeilennummern der Funktion aufschreiben
- Wir sehen, dass für die erste Reihe der Funktion gilt
- Also müssen wir es auch dort eintragen, wo sich alle drei schneiden
- Das wäre oben-links
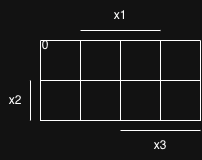
- Die nächste Zeile hat die Elemente
- Also müssen wir die Zeilennummer in der 1. Zeile und 2. Spalte eintragen, da sich dort diese Elemente schneiden
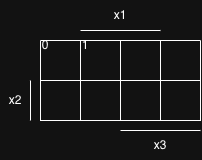
Dies führen wir fort, bis wir alle Zeilennummern eingetragen haben
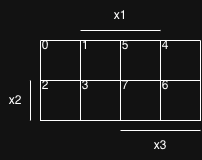
3. Wertigkeiten der Funktion eintragen
- Wir schauen dafür in die Tabelle und schauen jetzt erstmal in welchen Zeilen der Funktion sich die 0en befinden 0. Zeile, 1. Zeile, 4. Zeile und 7. Zeile
- Nun können wir die Nullen in die jeweiligen Nummern eintragen
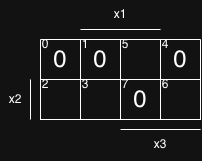
- Das selbe machen wir für die 1en 2. Zeile, 3. Zeile, 5. Zeile und 6. Zeile
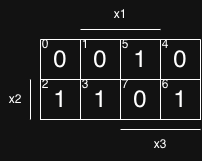
4. Nachbarn markieren
Nun müssen wir die aneinander gereihten Nachbarn markieren Dabei gilt:
- man markiert in Schritten. In diesem Beispiel können wir nur 2, 4 und 8 Nachbarn markieren
- man darf auch die Ecken miteinander verbinden
- man darf über das KV-Diagramm hinaus markieren. Man stelle sich vor, es sei eine Kugel
In unserem Fall können wir 2 Nachbarn markieren
- 2 und 3
- 2 und 6
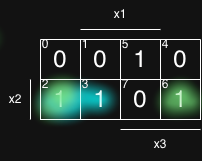
5. Elemente aufschreiben und Minterm bilden
- Für die 2 und 3 sehen wir, dass sie durch und dargestellt werden kann
- 2 und 6 kann durch und dargestellt werden
- die 5 ist alleine und wird durch und dargestellt